Bytes, Bits, Frequencies and Rise Time
 Quite often customers ask me, whether or not a connector would work for a certain set of electrical signals. Today everything is fast, especially the data rates. And whatever is above 1 Gbps is transmitted in differential pairs in order to get rid of common signal grounds and subsequent ground bounce which reduces the “readability” of the digital signal. And this is true inside the box between boards as well as outside the box going box-to-box with cables.With differential pair technology, we have to look into two things.
Quite often customers ask me, whether or not a connector would work for a certain set of electrical signals. Today everything is fast, especially the data rates. And whatever is above 1 Gbps is transmitted in differential pairs in order to get rid of common signal grounds and subsequent ground bounce which reduces the “readability” of the digital signal. And this is true inside the box between boards as well as outside the box going box-to-box with cables.With differential pair technology, we have to look into two things.
First we need to understand how to set up the pinning on the connector. If we use backplane connectors such as Impact™ or Impel™ for speeds above 6 Gbps, 10 Gbps or even 25 Gbps, we don’t have to think about pinning. The connector designers in cooperation with the signal integrity gurus have already considered the best way of packing the transmission lines into these connectors.
This is also true when we use I/O connectors such as SFP+, QSFP+ or iPass+™ HD running between 6 Gbps and 14 Gbps today and hopefully (on shorter distances) 25 Gbps tomorrow. The crux comes when one of these connectors is at the limit with regard to speed, when transmission links are getting longer, and when restrictions in cross talk or common mode transformation become critical.
If we have lower speeds or LVDS (Low Voltage Differential Signaling) we may use standard connectors with no dedicated pinning, but this is worth another blog!
Second we need to understand what a digital signal is all about, how it is composed and what the criteria are to fully understand the influence of a connection within the transmission line.
Let’s start with the basics which go back to Mr. Shannon and Mr. Fourier. The Shannon theorem says that the maximum you can do is to pack 2 bits into a full sine wave. This relates also to the digital NRZ (Non Return to Zero) coding. There are other semi-analog coding schemes like PAM4 where you have to read four different voltage levels out of your signal, but this is too deep for today. Just to let you know that the 10 Gigabit Ethernet transmission over an RJ-45 works this way.
Let’s stick with NRZ and wonder, why digital people like square wave signals: A square wave signal shows a clear “1” or “0” over a relatively long period of time and the change between the bits is fast and takes very little time. This gives you an advantage when transmitting many digital signals in parallel over a longer distance. You have a long open window to read your information even if the parallel digital links have different delays i.e. one travels faster than the other. This technique was used in the parallel printer ports when PCs were born and this is also the reason why printer cables were limited in length. People enjoyed the bandwidth (the data rate times the parallel links) but had to use single lane serial transmission for longer reaches with a much lower bandwidth.
Nowadays we overcome the issue of delay variation using a parallel serial transmission with 8B/10B resp. 64B/66B coding which reduces the amount of transmitted data by 20 respectively 5 percent but allows you to identify the correct single bits which belong to a byte even if they show up at different times.
Back to NRZ: How is a square wave generated?
To understand this we need to ask Joseph Fourier. He was a great mathematician and proved in the 19th century that any signal curve is a function of many superimposed sinusoidal waves from different frequencies and different amplitudes. So is a square wave a superposition of the base frequency with the 3rd harmonic, the 5th harmonic, the 7th harmonic and so on. If we look closer it is the base frequency plus one third amplitude of the 3rd harmonic, one fifth amplitude of the 5th harmonic, and one seventh amplitude of the 7th harmonic – all in sync.
You may conclude the higher odd harmonics have less influence to shape the square wave, but let’s have a closer look and create an Excel sheet in 1/100 steps of a sine wave and generate graphs:
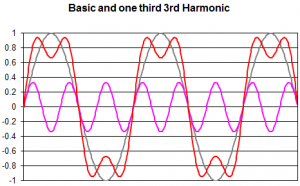
Base frequency plus one third of the 3rd harmonic:
Base frequency plus one third of the 3rd harmonic plus one fifth of the 5th harmonic:
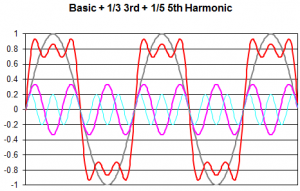
Base frequency plus 1/3 of 3rd harmonic plus 1/5 of 5th harmonic plus 1/7 of the 7th harmonic:

We recognize the superimposed “1” signal is always around 0.8 (or 80%) of the base frequency amplitude. The more odd harmonics we add to the superimposed signal the wider the square wave opens, however, we also see the signal rise at the zero line is steepening. This rise is the most critical item when the signal passes through a connector. Reason being that the connectors and vias are a disruption in the signal path and fast rises generate more crosstalk to the adjacent signal.
If we add more of the higher frequency odd harmonics, we need the signal path (PCB traces, vias, and connectors) being capable to transmit these higher frequencies. In order to keep everything efficient, we limit ourselves to look up to the 5th harmonic only. It shapes the signal close enough to a square wave and relaxes the requirements for the transmission line.
For example a 10 Gbps transmission line has a clock frequency (in NRZ per the Shannon theorem) of 5GHz, the 3rd harmonic is 15GHz, and the 5th harmonic is 25GHz. Therefor a 10 Gbps backplane connector shall be capable to transmit 25GHz although at a very small amplitude (one fifth of the base frequency signal level).
The bandwidth of the transmission line shall allow 25GHz to pass.
The rise time will be the superposition of the base frequency, the 3rd harmonic and the 5th harmonic.
A formula often found in the literature is
Rise time (in nanoseconds) = 0.35/bandwidth (in GHz)
or
Bandwidth (in GHz) = 0.35 / Rise time (in nanoseconds)
and it calculates the rise time for our 5th harmonic 25GHz signal at 14 picoseconds!
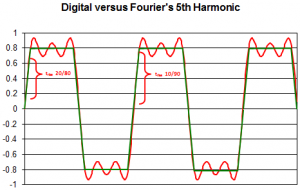
Going back into our Excel sheet and looking up the rise time (10% of the signal to 90% of the signal) of our 10 Gbps close-to-square-wave signal with the 5th harmonic, we find the time difference between y=0.08 (10% of “1” signal of 0.8) and y=0.72 (90% of “1” signal of 0.8) being 5.9 picoseconds.
If we take the absolute amplitude values (ignoring that the “1” signal is in reality not 1 but only 0.8) we come to a rise time from y=0.1 to y=0.9 of 12.8 picoseconds.
This tells us that the Bandwidth-to-Rise-Time formula above is not exact but close enough.
Unfortunately people tend to use 20/80 values because they look better but they are further away from the reality of Mr. Fourier’s analysis.
Why is rise time important at all? Because the digital world gives us tools to tune the rise time for the application. And rise time is like pharmacy: more than needed is most of the time no good!
So, if you can tune your rise time in the FPGA (or you have a choice between different chips with different rise times) have a look into your needs. Slower rise times reduce crosstalk when bumps are in the highway (impedance discontinuities in the transmission link).
The connector industry helps you with S-Parameters which shall reach out in frequency to include the 5th harmonic of your data rate. TDR data for the connectors should be done and compared with the actual rise time in your system. If you exaggerate your system by reducing the rise time, you may have to pay extra for a connector which complies with your rise time needs, but is not necessary when the system is designed the smooth way.
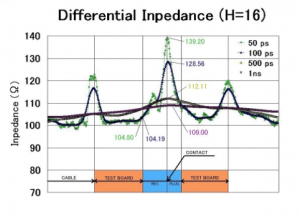
Recently I had a customer asking me why I took the 128Ω impedance and not 139Ω impedance (see below) when re-calculating a G S+ G S- G S+ G S- G structure into a G S+ S- G S+ S- G structure for a two-row SlimStack™ connector with 0.635mm spacing. I did it by purpose, because the customer had to handle a USB signal with “only” 480 Mbps which has a carrier of 240MHz and a 5th harmonic of 1.2GHz.
The rise time calculation shows 0.35 divided by 1.2GHz equals 0.291 nanoseconds or 291 picoseconds. Why should I consider 50 picoseconds rise time if it is not in his system?
So you see: Bytes and bits and frequency and rise time is no rocket science. Just liase with Joseph Fourier, take the 5th harmonic of the base frequency of your data rate and you will better understand what it is all about, what your real needs are and what your connectors must be capable to run!